Surface Integral
For a continuous Vector Point Function \(\vec{F} \) and 3-D surface S, its surface integral is given as \[ \iint_S \vec{F}.d\vec{S} \hspace{5pt} \text{ or } \hspace{5pt} \iint_S \vec{F}.\hat{N}ds \]
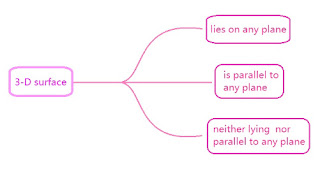
Now the question arises: how to find \(ds\) and \(\hat{N} \) from the 3-D surface. In surface integral, what we do is project the 3-D surface on one of the three planes X-Y, Y-Z or Z-X plane. So the value of \(ds\) depends on which plane the given 3-D surface will be projected. Here three cases arise,
.jpg)
In first two cases, the plane in which the surface is lying or parallel to will be used for \(ds\) and in third case you can choose to project in any plane you want. So calculation of \(ds\):
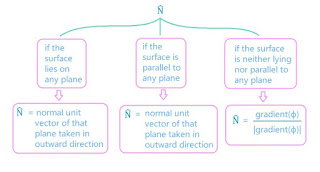
\(\hat{N} \) is normal unit vector outward to the surface. For calculation of \(\hat{N} \):
All of this is easy to remember: \(\hat{N} \) in first two cases is simply the normal unit vector of the plane in which the surface is lying. So for X-Y, Y-Z and Z-X planes, \(\hat{N} \) will be \(\hat{i}, \hat{j}, \hat{k} \) respectively. In third case, it is simply normal unit vector that you calculate with the help of gradient (if you need to revise gradient, Click Here ).
Some problems will help you clear everything.
Sample Problem 1
If \(\hspace{5pt} \vec{F} = -4y\hat{k} \hspace{5pt} \), find surface integral over the rectangle bounded by the lines \(\hspace{5pt} x = \pm a, y = 0, y = b \).
Solution
Let's trace the curve using given equations: \(\hspace{5pt} x = \pm a, y = 0, y = b \)
.jpg)
Surface Integral is given as: \[ \iint_S \vec{F}.\hat{N}ds \] Now since the given surface (rectangle) lies in X-Y plane so it must be projected in X-Y plane \[ ds = \frac{dxdy}{|\hat{N}\hat{k}|} \] \(\hat{N} = \) Normal Unit Vector of the surface so \[ \hat{N} = \hat{k} \] Putting all the values in the formula \[ \iint_S \vec{F}.\hat{N}ds = \int_0^b \int_{-a}^a (-4y\hat{k})\hat{N} \frac{dxdy}{|\hat{N}\hat{k}|} \] Limits of \(x\) are x-coordinates and limits of \(y\) are y-ccordinates \[ = \int_0^b \int_{-a}^a (-4y\hat{k})\hat{k} \frac{dxdy}{|\hat{k}\hat{k}|} \] \[ = \int_0^b \int_{-a}^a -4ydxdy \] \[ = \int_0^b \left[-4yx \right]_{-a}^a dy \] \[ = \int_0^b \left[-4y(a) - (-4y(-a)) \right]dy \] \[ = \int_0^b -8aydy = -8a\left[\frac{y^2}{2} \right]^b_0 \] \[ = \boxed{-4ab^2} \]