DC Network Theorems | Btech Shots!

DC Network Theorems

Some Basic Terms & Definitions

Electric Circuit : It is a closed path composed of active and passive elements in which electric current flows.

Active Element : It is the element in the circuit which provides energy to the circuit. Example- battery

Passive Element : It is the element in the circuit which receives energy and convert it to heat or stores it. Example- capacitor, resistor

Active Network : A network which contains one or more than one sources of e.m.f.

Passive Network : A network which contains no source of e.m.f.

Linear Circuit : A Linear circuit is one whose parameters are constant i.e. they do not change with voltage or current.

Non-Linear Circuit : It is that circuit whose parameters change with voltage or current.

Bilateral Elements : Elements which allow flow of current in both the directions.

Unilateral Elements : Elements which allow flow of current in only one direction.

Node : It is a point in a circuit where two or more elements are connected.

Junction : A point where three or more than three branches combine or the point where current divides.

Branch : is a part of a network which lies in between two junctions.

Loop : It is a closed path in a circuit in which no element or node is encountered more than once.

Mesh : It is a loop that contains no other loop within it.

Ohm's Law : The potential difference across any two points of conductor will be directly proportional to current flowing through it.
$V \propto I$ $V = I R$ Kirchoff's Laws:
1) Kirchoff's Voltage Law : (Based on Law of Conservation of Energy) In any closed circuit or mesh, algebraic sum of all EMFs and voltage drops is 0.
$\sum E M F s + \sum I R = 0$ Direction of Current
(a) If current is flowing from lower to higher potential ( $- v e$ to $+ v e$ ) $⟶$ Rise in potential $\Rightarrow$ current is positive
(b) If current is flowing from higher to lower potential ( $+ v e$ to $- v e$ ) $⟶$ Drop in potential $\Rightarrow$ current is negative

2) Kirchoff's Current Law : (Based on Law of Conservation of Charge) The algebraic sum of all the currents meeting at a point or a junction is 0. $\sum I = 0$
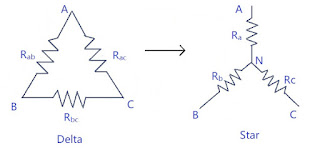
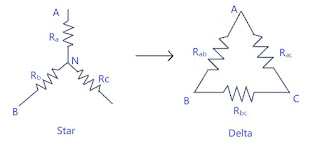
Star-Delta Transformation

Derivation :

Delta $⟶$ Star :

Between node $A$ and $B$ : $R_{a b} | | (R_{a c} + R_{b c})$ $\frac{R_{a b} \times (R_{a c} + R_{b c})}{R_{a b} + R_{a c} + R_{b c}} = R_{a} + R_{b} ⟶ (1)$ Between node $B$ and $C$ : $R_{b c} | | (R_{a b} + R_{a c})$ $\frac{R_{b c} \times (R_{a b} + R_{b c})}{R_{a b} + R_{a c} + R_{b c}} = R_{b} + R_{c} ⟶ (2)$ Between node $A$ and $C$ : $R_{a c} | | (R_{a b} + R_{b c})$ $\frac{R_{a c} \times (R_{a b} + R_{b c})}{R_{a b} + R_{a c} + R_{b c}} = R_{a} + R_{c} ⟶ (3)$ Adding equations 1, 2, 3 $2 (R_{a} + R_{b} + R_{c}) = 2 \frac{R_{a b} R_{b c} + R_{b c} R_{a c} + R_{a c} R_{a b}}{R_{a b} + R_{a c} + R_{b c}}$ $R_{a} + R_{b} + R_{c} = \frac{R_{a b} R_{b c} + R_{b c} R_{a c} + R_{a c} R_{a b}}{R_{a b} + R_{a c} + R_{b c}} ⟶ (4)$ Equation (4) - (1) $R_{c} = \frac{R_{a b} R_{b c} + R_{b c} a c + R_{a c} R_{a b}}{R_{a b} + R_{a c} + R_{b c}} - \frac{R_{a b} R_{a c} + R_{a b} R_{b c}}{R_{a b} + R_{b c} + R_{a c}}$ $R_{c} = \frac{R_{b c} R_{a c}}{R_{a b} + R_{b c} + R_{a c}} ⟶ (5)$ $R_{a} = \frac{R_{a b} R_{a c}}{R_{a b} + R_{b c} + R_{a c}} ⟶ (6)$ $R_{b} = \frac{R_{b c} R_{a b}}{R_{a b} + R_{b c} + R_{a c}} ⟶ (7)$

Star $⟶$ Delta :

Multiplying (7) and (6) $R_{a} \times R_{b} = \frac{R_{a b}^{2} \times R_{a c} \times R_{b c}}{(R_{a b} + R_{a c} + R_{b c})^{2}} ⟶ (8)$ Multiplying (6) and (5) $R_{a} \times R_{c} = \frac{R_{a c}^{2} \times R_{a b} \times R_{b c}}{(R_{a b} + R_{a c} + R_{b c})^{2}} ⟶ (9)$ Multiplying (5) and (7) $R_{b} \times R_{c} = \frac{R_{b c}^{2} \times R_{a c} \times R_{a b}}{(R_{a b} + R_{a c} + R_{b c})^{2}} ⟶ (10)$ Adding (8) (9) and (10) $R_{a} R_{b} + R_{b} R_{c} + R_{c} R_{a} = \frac{R_{a b}^{2} R_{a c} R_{b c} + R_{a c}^{2} R_{b c} R_{a b} + R_{b c}^{2} R_{a b} R_{a c}}{R_{b c}^{2} \times R_{a c} \times R_{a b}}$ $R_{a} R_{b} + R_{b} R_{c} + R_{c} R_{a} = \frac{R_{a b} R_{a c} R_{b c} (R_{a b} + R_{a c} + R_{b c})}{(R_{a b} + R_{a c} + R_{b c})^{2}}$ $R_{a} R_{b} + R_{b} R_{c} + R_{c} R_{a} = R_{a} \times R_{b c}$ $R_{b c} = \frac{R_{a} R_{b} + R_{b} R_{c} + R_{c} R_{a}}{R_{a}} ⟶ (11)$ Similarly $R_{a} R_{b} + R_{b} R_{c} + R_{c} R_{a} = R_{a b} \times R_{c}$ $R_{a b} = \frac{R_{a} R_{b} + R_{b} R_{c} + R_{c} R_{a}}{R_{c}} ⟶ (12)$ $R_{a} R_{b} + R_{b} R_{c} + R_{c} R_{a} = R_{a c} \times R_{b}$ $R_{a c} = \frac{R_{a} R_{b} + R_{b} R_{c} + R_{c} R_{a}}{R_{b}} ⟶ (13)$
Mesh Analysis

An important step in Mesh Analysis is identifying meshes so here is a quick example:

In this figure, $A B E F \to$ a Mesh $\to$ also a Loop
$B C D E \to$ a Mesh $\to$ also Loop
$A C D F \to$ not a Mesh $\to$ a Loop

Sample Problem 1 :

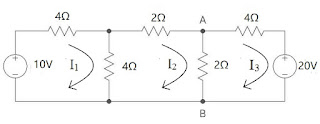
Calculate current in the branch of $2 Ω$ resistance for the given circuit using Mesh Analysis

Solution:

First we will identify meshes in the given circuit. There are three meshes in the circuit. In each mesh, current is flowing in clockwise direction.
Second apply KVL in mesh (1) : $+ 10 - 4 I_{1} - 4 (I_{1} - I_{2}) = 0$ $- 8 I_{1} + 4 I_{2} + 0 I_{3} = - 10 ⟶ (1)$ Applying KVL in mesh (2) : $- 4 (I_{2} - I_{1}) - 2 I_{2} - 2 (I_{2} - I_{3}) = 0$ $4 I_{1} - 8 I_{2} + 2 I_{3} = 0 ⟶ (2)$ Applying KVL in mesh (3) : $- 2 (I_{3} - I_{2}) - 4 I_{3} - 20 = 0$ $0 I_{1} + 2 I_{2} - 6 I_{3} = 20 ⟶ (3)$ Now, $A I = B, where I is current matrix$ $[\begin{matrix} - 8 & 4 & 0 \\ 4 & - 8 & 2 \\ 0 & 2 & - 6 \end{matrix}] [\begin{matrix} I_{1} \\ I_{2} \\ I_{3} \end{matrix}] = [\begin{matrix} - 10 \\ 0 \\ 20 \end{matrix}]$ Using Cramer's rule : $| \begin{matrix} A \end{matrix} | = - 8 (48 - 4) - 4 (- 24) = - 256$ $For I_{1}, A_{1} = [\begin{matrix} - 10 & 4 & 0 \\ 0 & - 8 & 2 \\ 20 & 2 & - 6 \end{matrix}]$ $| \begin{matrix} A_{1} \end{matrix} | = - 10 (- 4) - 4 (- 40) = 200$ $I_{1} = \frac{| \begin{matrix} A_{1} \end{matrix} |}{| \begin{matrix} A \end{matrix} |} = \frac{200}{- 256}$ $\Rightarrow I_{1} = - 0.781 A$ $For I_{2}, A_{2} = [\begin{matrix} - 8 & - 10 & 0 \\ 4 & 0 & 2 \\ 0 & 20 & - 6 \end{matrix}]$ $| \begin{matrix} A_{2} \end{matrix} | = - 8 (- 40) + 10 (- 24) = 80$ $I_{2} = \frac{| \begin{matrix} A_{2} \end{matrix} |}{| \begin{matrix} A \end{matrix} |} = \frac{80}{- 256}$ $\Rightarrow I_{2} = - 0.312 A$ $For I_{3}, A_{3} = [\begin{matrix} - 8 & 4 & - 10 \\ 4 & - 8 & 0 \\ 0 & 2 & 20 \end{matrix}]$ $| \begin{matrix} A_{3} \end{matrix} | = - 8 (- 160) - 4 (80) - 10 (8) = 880$ $I_{3} = \frac{| \begin{matrix} A_{3} \end{matrix} |}{| \begin{matrix} A \end{matrix} |} = \frac{880}{- 256}$ $\Rightarrow I_{3} = - 3.437 A$ Now current in the required $2 Ω$ branch will be equal to $I_{2} - I_{3}$ $I = I_{2} - I_{3} = - 0.312 + 3.437$ $I = 3.125 A$

Sample Problem 2 :

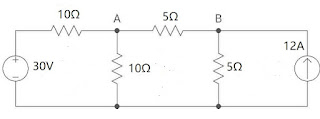
Find the current in $A - B$ using mesh analysis

Solution:

There are 3 meshes in the circuit
Applying KVL in mesh 1 : $30 - 10 I_{1} - 10 (I_{1} - I_{2}) = 0$ $- 20 I_{1} + 10 I_{2} = - 30$ $- 2 I_{1} + I_{2} = - 3 \Rightarrow (1)$ Applying KVL in mesh 2 : $- 10 (I_{2} - I_{1}) - 5 I_{2} - 5 (I_{2} - I_{3}) = 0$ $10 I_{1} - 20 I_{2} + 5 I_{3} = 0$ $2 I_{1} - 4 I_{2} + I_{3} = 0 \Rightarrow (2)$ Applying KVL in mesh 3, since there is only a current source : $I_{3} = - 12 A$ So putting the value in equation (2) : $2 I_{1} + 4 I_{2} = 12 \Rightarrow (3)$ Now, $A I = B, where I is current matrix$ $[\begin{matrix} - 2 & 1 \\ 2 & - 4 \end{matrix}] [\begin{matrix} I_{1} \\ I_{2} \end{matrix}] = [\begin{matrix} - 3 \\ 12 \end{matrix}]$ Using Cramer's rule : $| \begin{matrix} A \end{matrix} | = 8 - 2 = 6$ $For I_{1}, A_{1} = [\begin{matrix} - 3 & 1 \\ 12 & - 4 \end{matrix}]$ $| \begin{matrix} A_{1} \end{matrix} | = 12 - 12 = 0$ $I_{1} = \frac{| \begin{matrix} A_{1} \end{matrix} |}{| \begin{matrix} A \end{matrix} |} = \frac{0}{6}$ $\Rightarrow I_{1} = 0 A$ $For I_{2}, A_{2} = [\begin{matrix} - 2 & - 3 \\ 2 & 12 \end{matrix}]$ $| \begin{matrix} A_{2} \end{matrix} | = - 24 + 6 = - 18$ $I_{2} = \frac{| \begin{matrix} A_{2} \end{matrix} |}{| \begin{matrix} A \end{matrix} |} = \frac{- 18}{6}$ $\Rightarrow I_{2} = - 3 A$ $I_{A B} = I_{2} = - 3 A$
Nodal Analysis

Steps for solving numericals using Nodal Analysis :

1) Identify the principal nodes or junctions in the network
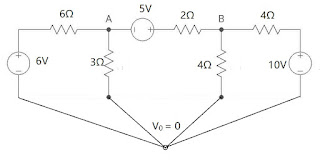
2) Pick a reference junction in the circuit with value $V_{0} = 0 V$
3) Assign a junction potential on each junction with respect to the reference junction
4) Assuming all the currents in outgoing (or incoming) direction from each junction, form KCL equations
5) Solve the equations and calculate value of the junction potentials
6) Using individual junction potentials find the value of required quantity

Sample Problem:

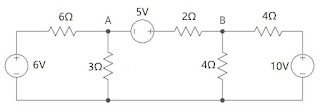
Find the current in $3 Ω$ resistor using Nodal Analysis

Solution:

Applying KCL at junction A : $I_{1} + I_{2} + I_{3} = 0$ $\frac{V_{A} - V_{0} - 6}{6} + \frac{V_{A} - V_{0}}{3} + \frac{V_{A} - V_{B} + 5}{2} = 0$ $\frac{V_{A} - V_{0} - 6 + 2 V_{A} - 2 V_{0} + 3 V_{A} - 3 V_{B} + 15}{6} = 0$ $6 V_{A} - 3 V_{B} = - 9$ $2 V_{A} - V_{B} = - 3 ⟶ (1)$ Applying KCL at junction B : $I_{1} + I_{2} + I_{3} = 0$ $\frac{V_{B} - V_{A} - 5}{2} + \frac{V_{B} - V_{0}}{4} + \frac{V_{B} - V_{0} - 10}{4} = 0$ $\frac{2 V_{B} - 2 V_{A} - 10 + V_{B} + V_{B} - 10}{4} = 0$ $- 2 V_{A} + 4 V_{B} = 20$ $- V_{A} + 2 V_{B} = 10 ⟶ (2)$ Now, $A V = B, where I is voltage matrix$ $[\begin{matrix} 2 & - 1 \\ - 1 & 2 \end{matrix}] [\begin{matrix} V_{A} \\ V_{B} \end{matrix}] = [\begin{matrix} - 3 \\ 10 \end{matrix}]$ Using Cramer's rule : $| \begin{matrix} A \end{matrix} | = 4 - 1 = 3$ $For V_{A}, A_{1} = [\begin{matrix} - 3 & - 1 \\ 10 & 2 \end{matrix}]$ $| \begin{matrix} A_{1} \end{matrix} | = - 6 + 10 = 4$ $V_{A} = \frac{| \begin{matrix} A_{1} \end{matrix} |}{| \begin{matrix} A \end{matrix} |} = \frac{4}{3} = 1.33 V$ $For V_{B}, A_{2} = [\begin{matrix} 2 & - 3 \\ - 1 & 10 \end{matrix}]$ $| \begin{matrix} A_{2} \end{matrix} | = 20 - 3 = 17$ $V_{B} = \frac{| \begin{matrix} A_{2} \end{matrix} |}{| \begin{matrix} A \end{matrix} |} = \frac{17}{4} = 4.25 V$ $I_{3 Ω} = I_{2} = \frac{V_{A} - V_{0}}{3}$ $I_{3 Ω} = 0.443 A$
Thevenin's Theorem

Thevenin's Theorem : It states that any linear bilateral network can be simplified into a Thevenin's equivalent circuit having Thevenin's open circuit voltage $V_{T h}$ in series with the Thevenin's equivalent resistance $R_{T h}$ along with load resistance $R_{L}$

$I_{L} = \frac{V_{T h}}{R_{L} + R_{T h}}$

Steps for solving :

1) Identify the load resistance $R_{L}$
2) Remove the load resistance and calculate the open circuit voltage across the two open ends $⟶ V_{T h}$
3) Again remove $R_{L}$ and replace all the active sources by their internal resistance: $\to for voltage source: Internal resistance = 0 \Rightarrow s h o r t - c i r c u i t$ $\to for current source: Internal resistance = \infty \Rightarrow o p e n - c i r c u i t$ 4) Calculate equivalent resistance across the open ends $\to R_{T h}$
5) Draw the Thevenin Equivalent circuit
6) Calculate load current $I_{L}$ by using $I_{L} = \frac{V_{T h}}{R_{L} + R_{T h}}$

Sample Problem

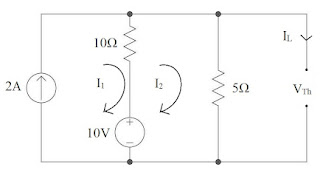
Find the current through $1 Ω$ resistor in given circuit using Thevenin's Theorem :

Solution :

Step 1: Load Resistance, $R_{L} = 1 Ω$
Step 2: Removing $R_{L}$ to find $V_{T h}$

Applying KVL in mesh 1 $I_{1} = 2 A$ Applying KVL in mesh 2 $10 - 10 (I_{2} - I_{1}) - 5 I_{2} = 0$ $10 - 10 (I_{2} - 2) - 5 I_{2} = 0$ $I_{2} = 2 A$ In mesh 3, for $5 Ω$ resistor, $V = I R = 2 \times 5 = 10 V$
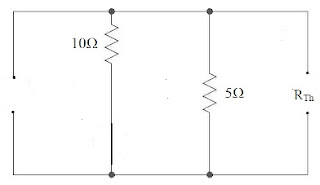
Applying KVL, $- V_{T h} + 10 = 0 \Rightarrow V_{T h} = 10 V$ Step 3: Removing $R_{L}$ and replacing all the acive sources by their internal resistance

Step 4: Equivalent Resistance across the open ends, $R_{T h} = 10 | | 5 = \frac{10 \times 5}{10 + 5} = \frac{50}{13} = 3.33 Ω$ Step 5: Thevenin's Equivalent circuit,

Sstep 6: Calculate Load Current, $I_{L} = \frac{V_{T h}}{R_{T h} + R_{L}} = \frac{10}{4.33}$ $I_{L} = 2.31 A$
Norton's Theorem

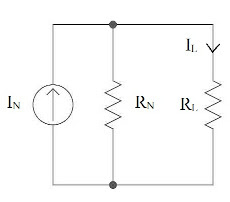
Norton's Theorem : Any linear bilateral network irrespective of its complexity can be reduced to Norton's Equivalent circuit having a Norton's short circuit current $I_{N}$ in parallel with Norton's equivalent resistance $R_{N}$ in parallel with load resistance $R_{L}$

$I_{L} = \frac{I_{N} R_{N}}{R_{N} + R_{L}}$

Steps for solving :

1) Identify the load resistance $R_{L}$
2) Replace $R_{L}$ with short circuited branch
3) The current flowing through this short circuit branch will be the Norton's current $I_{N}$
4) Remove $R_{L}$ and replace all the active sources by their internal resistance
5) The equivalent resistance across the two open ends will be the Norton's resistance $R_{N}$
6) Draw Norton's equivalent circuit
7) Calculate $I_{N}$ using identity : $I_{N} = \frac{I_{N} R_{N}}{R_{N} + R_{L}}$

Sample Problem :

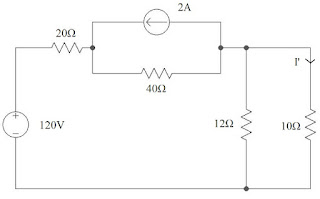
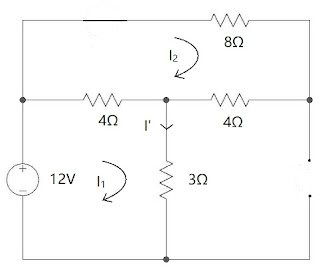
Find the current $I^{'}$ in the given circuit using Norton's Theorem :

Solution:

Step 1: Load Resistance, $R_{L} = 10 Ω$
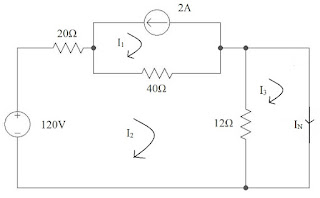
Step 2: Replacing $R_{L}$ with short circuit branch

Step 3: Finding $I_{N}$ ,
Applying KVL in mesh 1, $I_{1} = - 2 A$
Applying KVL in mesh 2, $120 - 20 I_{2} - 40 (I_{2} - I_{1}) - 12 (I_{2} - I_{3})$ $10 I_{1} - 18 I_{2} + 3 I_{3} = - 30$ $- 18 I_{2} + 3 I_{3} = - 10 ⟶ (1)$ Applying KVL in mesh 3, $- 12 (I_{3} - I_{2}) = 0$ $I_{2} = I_{3}$ In equation (1) $- 18 I_{2} + 3 I_{2} = - 10$ $I_{2} = 0.666 A$ $I_{N} = I_{3} = 0.666 A$ Step 4: Removing $R_{L}$ and replacing all active sources by their internal resistances

Step 5: Calculating Equivalent resistance, $R_{N} = (20 + 40) | | 12 = 60 | | 12 = 10 Ω$ Step 6: Norton's equivalent circuit,

Step 7: Calculate $I_{L}$ , $I_{L} = \frac{I_{N} R_{N}}{R_{N} + R_{L}} = \frac{0.666 \times 10}{10 + 10}$ $I_{L} = I^{'} = 0.333 A$
Superposition Theorem

Superposition Theorem : In any linear bilateral multisource network the current or voltage across any branch can be calculated by taking the algebraic sum of values calculated by taking one source at a time and replacing all the remaining sources by their internal resistances.

Steps for solving:

1) Identify the active sources and the quantity to be calculated
2) Consider any one active source and replace the remaining sources by their internal resistances
3) Calculate the required electrical quantity for that particular source
4) Repeat step 2 and 3 for remaining sources
5) Algebraic sum of all these individual values will be the final value of required electrical quantity for all the sources working together

Sample Problem :

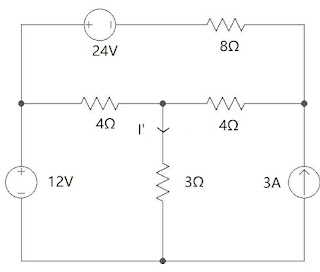
For given circuit calculate I' using Superposition Theorem:

Solution :

Step 1: There are two volatage sources and one current source
Step 2: Considering $12 V$ source and replacing the remaining sources with their internal resistances

Applying KVL in mesh 1, $12 V - 4 (I_{1} - I_{2}) - 3 I_{1} = 0$ $- 7 I_{1} + 4 I_{2} = - 12 ⟶ (1)$ Applying KVL in mesh 2, $- 8 I_{2} - 4 I_{2} - 4 (I_{2} - I_{1}) = 0$ $I_{1} = 4 I_{2}$ Putting $I_{1}$ in equation (1) $- 28 I_{2} + 4 I_{2} = - 12$ $I_{2} = 0.5 A$ $I_{1} = 2 A$ $I_{12 v} = I_{1} = 2 A$
Taking $24 V$ source and replacing the remaining sources with their internal resistances

Applying KVL in mesh 1, $- 3 I_{1} - 4 (I_{1} - I_{2}) = 0$ $I_{2} = \frac{7 I_{1}}{4}$ Applying KVL in mesh 2, $- 24 - 8 I_{2} - 4 I_{2} - 4 (I_{2} - I_{1}) = 0$ $- 16 I_{2} + 4 I_{1} = 24$ $- 28 I_{1} + 4 I_{1} = 24$ $I_{!} = - 1 A$ $I_{2} = \frac{- 7}{4}$ $I_{2} = - 1.75 A$ $I_{24 V} = I_{1} = - 1 A$
Taking $3 A$ source and replacing the remaining sources with their internal resistances

Applying KVL in mesh 2, $I_{2} = - 3 A$ Applying KVL in mesh 1, $- 4 (I_{1} - I_{3}) - 3 (I_{1} - I_{2}) = 0$ $- 7 I_{1} + 4 I_{3} = 9 ⟶ (1)$ Applying KVL in mesh 3, $- 8 I_{3} - 4 (I_{3} - I_{2}) - 4 (I_{3} - I_{1}) = 0$ $4 I_{1} - 16 I_{3} = 12$ $I_{1} - 4 I_{3} = 3 ⟶ (2)$ $[\begin{matrix} - 7 & 4 \\ 1 & - 4 \end{matrix}] [\begin{matrix} I_{1} \\ I_{3} \end{matrix}]$ $| \begin{matrix} A \end{matrix} | = 28 - 4 = 24$ $A_{1} = [\begin{matrix} 9 & 4 \\ 3 & - 4 \end{matrix}]$ $| \begin{matrix} A_{1} \end{matrix} | = - 36 - 12 = - 48$ $I_{1} = \frac{- 48}{24} = - 2 A$ $A_{2} = [\begin{matrix} - 7 & 9 \\ 1 & 3 \end{matrix}]$ $| \begin{matrix} A_{1} \end{matrix} | = - 21 - 9 = - 30$ $I_{3} = \frac{- 30}{24} = - 1.25 A$ $I_{2} = - 3 A$ $I_{3 A} = I_{1} - I_{2}$ $I_{3 A} = 1 A$ Total Current, $I_{T} = I_{12 V} + I_{24 V} + I_{3 A}$ $I_{T} = 2 A$
Maximum Power Transfer Theorem

Maximum Power Transfer Theorem : The condition for maximum power flow through load resistor $R_{L}$ can be acheived when the load resistor equals the Thevenin's equivalent resistance of the circuit.

Power through $R_{L}$ $P = I_{l}^{2} R_{L}$ $I_{L} = \frac{V_{T h}}{R_{T h} + R_{L}}$ $P = (\frac{V_{T h}}{R_{T h} + R_{L}})^{2} R_{L}$ Differentiating above equation with respect to $R_{L}$ and equating it to 0 $\frac{d P}{d R_{L}} = V_{T h}^{2} [\frac{(R_{T h} + R_{L})^{2} - 2 R_{L} (R_{T h} + R_{L})}{(R_{T h} + R_{L})^{4}}]$ $R_{T h}^{2} - R_{L}^{2} = 0$ $R_{T h} = R_{L}$ This is the condition for maximum power flow $P = (\frac{V_{T h}}{R_{T h} + R_{L}})^{2} R_{L}$ $= \frac{V_{T h}^{2}}{4 R_{T h}^{2}} \times R_{T h}$ $P_{m a x} = \frac{V_{T h}^{2}}{4 R_{T h}}$

Sample Problem:

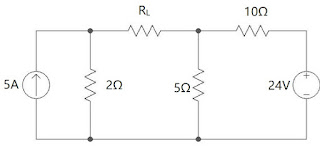
In the given network find the value of $R_{L}$ which will absorb the maximum power from the source. Also find the maximum power.

Solution

For $V_{T h}$ , removing $R_{L}$

Applying KVL in mesh 1: $I_{1} = 5 A$ Applying KVL in mesh 2: $- 5 I_{2} - 10 I_{2} = 24 V$ $I_{2} = - 1.6 A$ $- V_{T h} - 8 + 10 = 0$ $V_{T h} = 2 V$ Removing $R_{L}$ and replacing all active sources with their internal resistances

$R_{T h} = 2 + 5 | | 10$ $R_{T h} = 2 + \frac{50}{15}$ $R_{T h} = 5.33 Ω$ For maximum power flow, $R_{L} = R_{T h} = 5.33 Ω$ $P_{m a x} = \frac{V_{T h}^{2}}{4 R_{T h}}$ $P_{m a x} = \frac{4}{4 \times 5.33}$ $P_{m a x} = 0.187 W$