Equivalent Circuit of Transformer
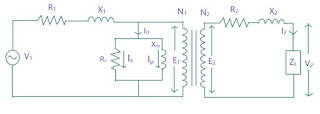
The concept of Equivalent Circuits exists to help us analyze transformer as by using this concept, we can transform all the parameters to either side. When referred to primary side, it is called Equivalent Circuit referred to primary side and when referred to secondary side, it is called Equivalent Circuit referred to secondary side.
.jpg)
Here \( I_1 = I_0 + I'_2 \)
The no load primary current \(I_0\) is very small in comparison to full load current around 2% to 5% of full load current. So,
\[ I_1 \approx I'_2 \]
So we will interchange the core loss and leakage flux loss part with the winding losses part as shown in the diagram. This is called Approximate Equivalent Circuit.
The core losses and flux losses are negligible, so we will remove them to further simply the circuit,
Now we can perform calculations:
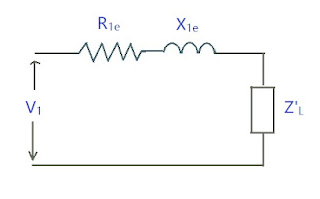
Equivalent Circuit referred to Primary Side
This means shifting all the elements to the primary side.
\(R_{1e} \) is Equivalent resistance referred to primary
\(X_{1e} \) is Equivalent reactance referred to primary
Before we get into equations for equivalent resistance and reactance, get this formula for relation between resistance and turn ratio:
\[ V_1 = I_1R_1 , V_2 = I_2R_2\]
\[ \frac{V_1}{V_2} = \frac{I_1R_1}{I_2R_2} \]
\[ \frac{R_1}{R_2} = \frac{V_1I_2}{V_2I_1} = \frac{N_1}{N_2}\frac{N_1}{N_2} \]
\[ \frac{R_1}{R_2} = \left(\frac{N_1}{N_2} \right)^2 \]
So if \(R_2\) is to be referred from secondary to primary side, then it will be written as
\[ R_2\left(\frac{N_1}{N_2}\right)^2 \]
And if \(R_1\) is to be referred from primary to secondary side, then it will be written as
\[ R_1\left(\frac{N_2}{N_1}\right)^2 \]
So writing equations for equivalent resistance and reactance,
\[ R_{1e} = R_1 + R_2\left(\frac{N_1}{N_2} \right)^2 \]
\[ X_{1e} = X_1 + X_2\left(\frac{N_1}{N_2} \right)^2 \]
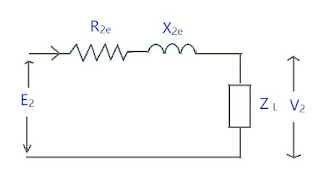
Equivalent Circuit referred to Secondary Side
This means shifting all the elements to the secondary side.
\(R_{2e} \) is Equivalent resistance referred to secondary
\(X_{2e} \) is Equivalent reactance referred to secondary
\[ R_{2e} = R_2 + R_1\left(\frac{N_2}{N_1} \right)^2 \]
\[ X_{2e} = X_2 + X_1\left(\frac{N_2}{N_1} \right)^2 \]