DC Motor, Basic Electrical Engineering, Btech first year

DC Motor

Working Principle

The principle on which DC Motor works is:

"When a current carrying conductor is placed in a magnetic field, it experiences a mechanical force"

The construction of both DC Generator and Motor is same, the only difference is here we provide energy to the machine. As we excite the armature, the conductors of the armature, placed in magnetic field, experience a mechanical force and the motor starts moving. The direction of rotation is given by Fleming Left Hand Rule.

"Outstretch three fingers of left hand namely first finger, middle finger and thumb such that they are mutually perpendicular to each other. If we point first finger in direction of magnetic field and middle finger in direction of current, then the thumb gives direction of force experienced by the conductor."

Back EMF

Once motor starts rotating its conductor will cut magnetic flux produced by field winding, so by Faraday's Law of Electromagnetic Induction there will be induced emf just like in case of emf induced in dc generator. This emf is called Back emf. \[ \boxed{E_b = \frac{\phi PNZ}{60A} } \] The role of back emf in starting and running of the motor is important. The presence of back emf makes the DC Motor a self-regulating machine i.e. it makes the dc motor to draw as much armature current as is sufficient to develop the required load torque.

\[ V_t = I_aR_a + E_b + V_{brush} \] V_t is the supply voltage and it has to take care of all the three factors.

Torque Equation of DC Motor

      Mechanical Power = Torque × Angular Velocity
\[ P = T \times \omega \] \[ E_bI_a = T \times \frac{2\pi N}{60} \] \[ \frac{\cancel{N}P\phi Z}{\cancel{60}A} \times I_a = T \times \frac{2\pi \cancel{N}}{\cancel{60}} \] \[ \boxed{T = \frac{1}{2\pi}\phi I_a \frac{PZ}{A} } \] \[ \boxed{T = 0.159 \phi I_a \frac{PZ}{A} } \] The unit is Newton-meter (Nm).

Types of DC Motor

There are three types of motors:

1) Series Motor
2) Shunt Motor
3) Compound Motor : Of 2 types
      a) Long Shunt Compound Motor
      b) Short Shunt Compound Motor

The construction of all these types are similar to dc generator.

DC Series Motor

\[ I_L = I_{se} = I_a \] \[ E_b + I_aR_a + I_{se}R_{se} - V_t = 0 \] \[ E_b + I_aR_a + I_aR_{se} - V_t = 0 \] \[ E_b + I_a(R_a + R_{Se}) - V_t = 0 \] \[ \boxed{V_t = E_b + T_a(R_a + R_{se}) + V_{brush} } \]

DC Shunt Motor

\[ I_L = I_{sh} + I_a \] \[ E_b + I_aR_a - V_t = 0 \] \[ \boxed{V_t = E_b + I_aR_a } \] \[ \boxed{I_{sh} = \frac{V_t}{R_{sh}} = \frac{E_b + I_aR_a}{R_{sh}} } \]

Compound DC Motor

Long Shunt

\[ I_L = I_{se} + I_{sh} \] Or \[ I_L = I_a + I_{sh} \] \[ E_b + I_aR_a + I_{se}R_{se} - V_t = 0 \] \[ \boxed{V_t = E_b + I_aR_a + I_{se}R_{se} } \] \[ \boxed{I_{sh} = \frac{V_t}{R_{sh}} = \frac{E_b + I_a(R_a + R_{se})}{R_{sh}} } \]

Short Shunt

\[ I_L = I_{se} \] \[ I_L = I_{se} = I_a + I_{sh} \] \[ E_b + I_aR_a + I_{se}R_{se} - V_t = 0 \] \[ \boxed{V_t = E_b + I_aR_a + I_{se}R_{se} } \] \[ \boxed{I_{sh} = \frac{V_t}{R_{sh}} = \frac{E_b + I_aR_a + I_{se}R_{se}}{R_{sh}} } \]

DC Generator, Basic Electrical Engineering, Btech first year

DC Generator

Principle of Operation

Basically, the principle of DC Generator is based on dynamically induced emf i.e. Faraday's Law of Electromagnetic Induction. This law states that :

"Whenever the magnetic flux linking with a conductor changes, an Electromagnetic Force (EMF) is set up in that conductor."

\[ \text{Dynamically induced emf }, e = \frac{d\phi}{dt} \] The direction of flux is given by Right Hand Thumb Rule which states that "if the thumb of the right hand represents direction of current then direction of the curled fingers represent direction of flux".

Now the question arise, how do we change the flux? The answer is relative motion between the conductor and the flux. So there are two ways to do that:

1) Keep the conductor stationary and move the flux
2) Keep the flux stationary and move the conductor

In DC generator, we keep the flux stationary and move the conductor. The device that moves this conductor is called Prime Mover. Some examples of Prime Mover are: diesel engine, diesel turbine, steam turbine etc.

Now the next question arises, what is the direction of this induced emf? For that we have Fleming's Right Hand Rule:

"If the three fingers of right hand, namely thumb, index finger and middle finger are outstretched so that each one of them is at right angles with the remaining two and if in this position the index finger is made to point in the direction of flux, thumb in the direction of the relative motion of conductor w.r.t. flux then the outstretched middle finger gives the direction of induced emf in the conductor"

While in DC Motors, the rule used is Fleming's Left Hand Rule (not right hand rule).

The emf induced is alternating in nature. So the question arises: if the induced emf is alternating, how is it a DC Generator? The answer is a rectifier called as Commutator. This device is not electronic, instead its entirely mechanical.

"Commutator is a device used in DC Generator to convert alternating induced emf to unidirectional DC emf"

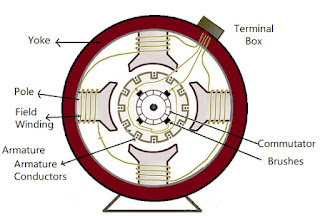
Construction

The construction remains same for both generator and motor.

Yoke : It is the outermost protective cover of the machine. It protects all the components from dust, moisture etc. It serves as a mechanical support to the parts. It also provides low reluctance path for the flux, so its made up of Cast Iron as it is a magnetic material.

Pole : The pole has two parts:

     Pole Core : It carries field windings which are responsible for production of magnetic flux.
     Pole Shoe : It covers the maximum armature conductor to cut flux so that we have maximum induced emf.
As flux passes through it, it should provide a low reluctance path so it is made up of Cast Iron.

Field Winding : It is the coil or wire that carries the current which is responsible for the production of flux. It is made up of Copper.

Armature : That part where the emf is induced. It is made up of Cast Iron.
  Armature Conductor : That part which takes the voltage or current out of armature to the commutator

Commutator : That part which rectifies AC emf to DC.

Brushes : It takes out the voltage or current from the Commutator to the terminals. It is made up of Carbon.

Emf Equation of DC Generator

Before we derive the emf equation, let's define some terms:
Let P = number of poles in the generator
φ = flux produced by each pole
N = speed of armature of generator (in rpm)
Z = total number of conductors in armature
A = number of parallel paths in which armature conductors are distributed
So by Faraday's Law of Electromagnetic Induction:
      e = Rate of cutting of the flux
\[ e = \frac{d\phi}{dt} \]     Total flux = Flux produced by each pole × number of poles
    So, total flux = φ × P
    Time required to complete one revolution = 60/N
\[ e = \frac{\phi P}{\large\frac{60}{N}} \] \[ e = \frac{\phi PN}{60} \] This emf is for one conductor
As Z conductors are distributed in A parallel paths, effective number of conductors will be Z/A, so \[ E = \frac{\phi PN}{60}\times\frac{Z}{A} \] \[ \boxed{E = \frac{\phi PNZ}{60A} } \]

Types of Generators

On the basis of Excitation of field winding, there are two types of generators:
1) Seperately Excited Generator
2) Self Excited DC Generator

Seperately Excited Generator

A DC Generator whose field winding or coil is energised by a seperate or external DC source is called a seperately excited DC Generator.

Self Excited Generator

Self-excited generators are the generators which get excited with the initial current in the field coils.

What actually happens is: there is a small amount of magnetism present in the rotor iron. This residual magnetic field of the main poles, induces an emf in the stator coils, which produces initial current in the field windings.

Due to flow of small current in the coil, an increase in magnetic field occurs. As a result, voltage output increases,which in turn, increases the field current. This process continues as long as the emf in the armature is more than the voltage drop in the field winding. But after at certain level, field poles get saturated and at that point electric equilibrium is reached, and no further increase in armature emf and increase in current takes place.

Based on the connection of field winding to the armature, there are 3 types of generator

1) Series Generator
2) Shunt (Parallel) Generator
3) Compound Generator : Of 2 types
      a) Long Shunt Compound Motor
      b) Short Shunt Compound Motor

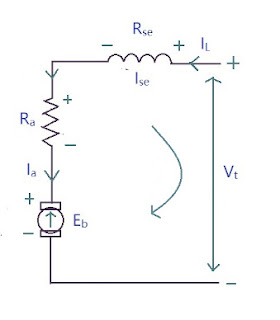
Series Wound Generator

In series wound generators, field winding and the armature winding are connected in series so that current that passes through external circuit and through field windings, passes from armature.

The field coil of series-wound generator has low resistance, and consists of a few turns of thick wire. If the load resistance decreases, then the current flow increases. As a result magnetic field and output voltage increases in the circuit. In such generators, output voltage varies directly with respect to load current which is not required in most of the applications. Due to this, it is not used a lot.

\[ I_{se} = I_a = I_L \]
Applying KVL we get, \[ E_g - I_aR_A - I_{se}R_{se} - V_t = 0 \] \[ E_g = V_t + I_aR_A + I_{se}R_{se} + V_{brush} \] \[ \boxed{E_g = V_t + I_a(R_a + R_{se}) + V_{brush}} \] where I_aR_a is Armature resistance drop, E_b is back emf and V_brush is brush resistance drop

Shunt Wound DC Generators

In this type of generator, the field winding is wired parallel to the armature winding so that voltage is same across the circuit.

Here, field winding has many numbers of turns for the desired high resistance so that fewer armature current can pass through the field winding and the remaining passes through load.

In shunt wound generator, the output voltage is almost constant and if it varies then it varies inversely with respect to load current.

\[ I_a = I_{sh} + I_L \] \[ E_g - T_aR_a - V_t = 0 \] \[ \boxed{E_g = V_t + I_aR_a + V_{brush} } \] \[ \boxed{I_{sh} = \frac{V_t}{R_{sh}} = \frac{E_g - I_aR_a}{R_{sh}} } \]

Compound Generator

Compound Wound Generator is the best of both worlds i.e. series and shunt wound generators. On the basis of their connection they are of two types:

1) Long Shunt Compound Generator
2) Short Shunt Compound Generator

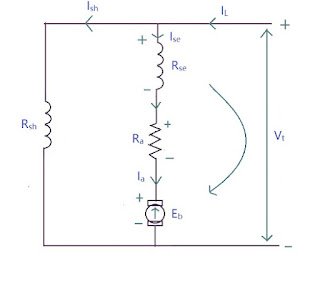
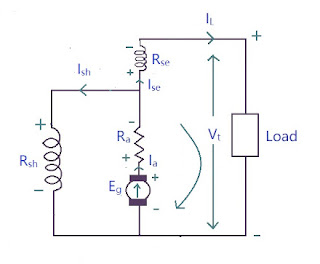
Long Shunt Compound Generator

The connection is made as shown in the diagram:

\[ I_{se} = I_a = I_{sh} = I_L \] \[ E_g = V_t + I_aR_a + I_{se}R_{se} + V_{brush} \] \[ = V_t + I_aR_a + I_{a}R_{se} + V_{brush} \] \[ \boxed{E_g = V_t + I_a(R_a + R_{se}) + V_{brush} } \] \[ \boxed{I_{sh} = \frac{V_t}{R_{sh}} = \frac{E_g - I_a(R_a + R_{se})}{R_{sh}} } \]

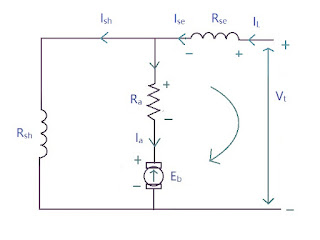
Short Shunt Compound Generator

The connection is made as shown in the diagram:

\[ I_{se} = I_L \] \[ I_a = I_{sh} + I_{se} \] \[ E_g - I_aR_a - I_{se}R_{se} - V_t = 0 \] \[ \boxed{E_g = V_t + I_aR_a + I_{se}R_{se} + V_{brush} } \] \[ \boxed{I_{sh} = \frac{V_t}{R_{sh}} = \frac{E_g - I_aR_a - I_{se}R_{se}}{R_{sh}} } \]

3 Phase Induction Motor, Basic Electrical Engineering, Btech first year

3 Phase Induction Motor

Construction

To understand its principle we need to know its construction. It has mainly two parts:

1) Stator
2) Rotor

Stator

It is the stationary part of the machine. It ha windings called Stator winding. 3-phase supply is provided to these windings. It also provides mechanical strength to the machine.

Rotor

It is a rotatory part of Induction motor. It has windings called Rotor winding. The conductors are placed on the periphery of the rotor.

On the basis of applications of Induction Motor they are of two types:

1) Slip Ring or Wound Rotor
2) Squirrel Cage Rotor

Squirrel Cage Rotor

Squirrel Cage Rotors are used where constant speed is required. In this type, both the end rings are permanently short-circuited. The conductors made up of Aluminium and Copper are placed between the end rings hence these are also short-circuited.
Hence the overall resistance of the rotor is constant and is used for the constant speed application. Example: Elevators.

Slip Ring or Wound Rotor

This type of rotor construction is used where high starting torque is required.
In this type of rotor, Aluminium and Copper conductors are connected with the external Rheostat so that by varying resistance, the overall resistance of the rotor can be varied.

Working Principle

When 3 phase supply is given to the stator winding, a rotating magnetic field with speed called as Synchronous Speed (N_s) is generated. It rotates in clockwise direction.

As the magnetic field is rotating and the conductors are stationary, due to relative motion between magnetic flux and conductor, magnetic field gets cut and an emf is induced. Hence current starts flowing in rotor winidng.

Now as the conductors are current carrying and is placed in magnetic field, a torque is exerted on the rotor and the rotor starts to rotate in clockwise direction with a speed called as rotor speed.

Let's define some basic terms that we use with induction motor.

Slip Speed

It is the difference between Synchronous speed and rotor speed. \[ \text{Slip Speed } = N_S - N_R \]

Slip

It is defined as the ratio of Slip Speed to the Synchronous speed. \[ S = \frac{N_S - N_R}{N_S} \]
1) When the motor is standing still \[ N_R = 0 \Rightarrow \boxed{S = 1} \] 2) at N_R = N_S \[ \boxed{S = 0} \]

Applications

Induction motor is used in fans, vaccum cleaners, washing machines, centrifugal pumps etc.

Electrical Machines, Basic Electrical Engineering, Btech first year

Electrical Machines

Topics that we are going to study in this unit:

DC Generator DC Motor 3 Phase Induction Motor

Principle of Transformer & its emf equation, Basic Electrical Engineering, Btech first year

Principle & Emf Equation of Transformer

Transformer is a device that is used to transfer electrical energy from one circuit to another using the phenomena of Mututal Induction. Keeping the energy conserved (it does not generate energy), it is used to increase or decrease voltage.

Working Principle

A basic transformer consists of two coils (or windings), one coil is connected to power supply. This power supply is alternating in nature (transformers don't work on dc). The alternating current passed through the coil generates flux which is also alternating in nature. Some part of this flux links with the second coil. As it is continuously changing, there must be a changing flux linkage in the second coil due to Mututal Induction. This changing flux in the second coil generates emf in the coil.

Primary Winding

The winding to which energy is supplied and generates flux to be transferred to second coil is called Primary Winding.

Secondary Winding

The winding in which emf is induced due to the flux transferred from the primary winding is called Secondary Winding. This gives us the desired output voltage.

However, this isn't how the transformers are built because a lot of flux does not get linked with the secondary winding and it gets wasted. In real transformer, this wastage of flux should be as minimum as possible, for that purpose core is used.

Core

The core provides a low reluctance path, through which maximum amount of flux generated by primary winding is passed and linked with the secondary winding.

So basically the transformer consists of 3 main parts: Primary Winding, Core and Secondary Winding.

Emf Equation

Let the primary winding of the transformer is connected to power supply. As a result of which flux \(\phi \) is generated in the primary winding. This flux is alternating in nature therefore, \[ \phi = \phi _m\sin{\omega t} \]

By Faraday's Law of Electromagnetic Induction and Lenz's Law: \[ e = -N \frac{d\phi}{dt} \] Emf induced at primary side: \[ e_1 = N_1 \frac{d\phi}{dt} \] where \(N_1\) is number of turns in primary winding \[ \Rightarrow e_1 = -N_1\frac{d(\phi_m \sin{\omega t})}{dt} \] \[ e_1 = -N_1\omega \phi_m \cos{\omega t} \] \[ e_1 = N_1\omega \phi_m (-\cos{\omega t}) \] \[ -\cos{\omega t} = \sin{(\theta - 90^o)} ,\hspace{20pt} \omega = 2\pi f \] \[ e_1 = \phi_m 2\pi fN_1 \sin{(\omega t -90^o)} \] Comparing with standard equation of emf \[ e_1 = E_{m1}\sin{(\omega t + \psi)} \] \[ E_{m1} = 2\pi f \phi_m N_1, \hspace{15pt} \psi = -90^o \] RMS value of emf = \(\frac{E_{m1}}{\sqrt{2}} \) \[ = \frac{2\pi f \phi_m N_1}{\sqrt{2}} \] \[ \boxed{E_1 = 4.44 \phi_m f N_1 } \] Similarly secondary side emf: \[ \boxed{E_2 = 4.44 \phi_m f N_2 } \] As \(\psi = -90^o \Rightarrow E_1 \text{ and } E_2 \) lag flux \(\phi \) by 90^o

Phasor Diagram

Ratios in a Transformer

\[ E_1 = 4.44 \phi_m f N_1 \] \[ E_2 = 4.44 \phi_m f N_2 \] \[ \frac{E_1}{E_2} = \frac{4.44 \phi_m f N_1}{4.44 \phi_m f N_2} \] \[ \boxed{\frac{E_1}{E_2} = \frac{N_1}{N_2} } \] If we neglect resistance and leakage reactance \[ E_1 \approx V_1 \text{ & } E_2 \approx V_2 \] \[ \boxed{\frac{E_2}{E_1} = \frac{V_2}{V_1} = \frac{N_2}{N_1} = K \text{ (Turns ratio)} } \] It is also called as Voltage Ratio

Primary side power = Secondary side power \[ \Rightarrow V_1I_1 = V_2I_2 \] \[ \frac{V_2}{V_1} = \frac{I_1}{I_2} \] \[ \boxed{\frac{V_2}{V_1} = \frac{I_1}{I_2} = \frac{N_2}{N_1} = K } \] It is called as current ratio

Step Up & Step Down Transformer

In Step Up Transformer, voltage on the secondary side is greater than voltage on the primary side \[ V_2 > V_1 \] \[ \Rightarrow K > 1 \] \[ \Rightarrow I_1 > I_2 \] In Step Down Transformer, voltage on the primary side is greater than voltage on the secondary side \[ V_1 > V_2 \] \[ \Rightarrow K \lt 1 \] \[ \Rightarrow I_2 > I_1 \]

Losses & Efficiency in a Transformer, Basic Electrical Engineering, Btech first year

Losses & Efficiency in a Transformer

Losses in Transformer

Loss in any machine is when your output is lesser than the input you gave. In transformer this is loss is in terms of power. As it is a static device, there are only electrical losses in a transformer, unlike a motor which also has mechanical losses. All types of losses are:

(a) Core Losses or Iron Losses

Losses occuring in the core of the transformer. These are:

Hysteresis loss in transformer : Hysteresis loss occurs when there is reversal in the process of magnetization in the transformer core. This loss depends upon the volume and grade of the iron, value of flux density and frequency of magnetic reversals.

Eddy Current Loss in transformer : In transformer, AC current is supplied to the primary winding which sets up alternating magnetizing flux. When this flux links with secondary winding, it produces induced emf in it. But some part of this flux also gets linked with other conducting parts like steel core or iron body, which results in induced emf in those parts, resulting in small circulating currents in them. This current is called as Eddy current. Due to these eddy currents, some energy is dissipated in the form of heat causing Eddy current loss in transformer.

(b) Copper Loss

Copper loss occurs due to the resistance of the windings of the transformer. For primary winding, it is \(I_1^2R_1 \) and for secondary winding, it is \(I_2^2R_2\) where \(I_1 \) is primary current, \(R_1\) is primary winding resistance, \(I_2\) is secondary current and \(R_2\) is secondary winding resistance. As you can see, Copper loss is directly proportional to square of current and current depends on load, it implies that copper loss varies with the load connected to the transformer.

Efficiency of Transformer

Efficiency is given by ratio of output power to the input power.
Transformers are the most highly efficient electrical machines. Most of the transformers have full load efficiency between 95% to 98.5% .
As due to high efficiency, output is nearly equal to input power, so it becomes an impractical to measure efficiency using ratio of output and input. So a better way is to calculate the losses, subtract them from input and then calculate the ratio, \[ \text{Efficieny } = \frac{\text{Input - Losses}}{\text{Input}} \]

Condition for Maximum Efficiency

Input Power \( = V_1I_1\cos{\phi_1} \)
Let,
Copper Loss \( = I_1^2R_1 \)
Iron Loss \( = W_i\) \[ \text{Efficiency } = 1 - \frac{\text{Losses}}{\text{Input}} \] \[ \eta = 1 - \frac{I_1^2R_1 + + W_i}{V_1I_1\cos{\phi_1}} \] \[ \eta = 1 - \frac{I_1^2R_1}{V_1I_1\cos{\phi_1}} - \frac{W_i}{V_1I_1\cos{\phi_1}} \] Differentiating w.r.t. \(I_1\) \[ \frac{d\eta}{dI_1} = 0 - \frac{R_1}{V_1\cos{\phi_1}} + \frac{W_i}{V_1I_1^2\cos{\phi_1}} \] \(\eta\) will be maximum at \(\large\frac{d\eta}{dI_1} = 0 \)
So, \[ \frac{R_1}{V_1\cos{\phi_1}} = \frac{W_i}{V_1I_1^2\cos{\phi_1}} \] \[ \frac{I_1^2R_1}{V_1I_1^2\cos{\phi_1}} = \frac{W_i}{V_1I_1^2\cos{\phi_1}} \] \[ \boxed{I_1^2R_1 = W_i} \] Hence the efficiency of the transformer will be maximum when copper loss is equal to the iron loss.

Ideal & Practical Transformer, Basic Electrical Engineering, Btech first year

Ideal & Practical Transformer

Ideal Transformer

A ideal transformer is an imaginary transformer which has:

• -> no copper losses
• -> no iron loss in the core
• -> no leakage flux

More on losses Here
In ideal transformer, input power = output power. Concept of such transformer exists to make problems easier.

Characteristics of Ideal Transformer

Zero Winding Resistance : Resistance of both primary and secondary winding is 0 i.e. both the coils are purely inductive in nature.

100% Efficiency : There are no losses in ideal transformer so the input power = output power \(\Rightarrow E_1I_1 = E_2I_2 \)

No leakage flux : The whole amount of flux is linked from primary to secondary winding, so there is no leakage flux.

No Iron loss : As the iron core is subjected to alternating flux there occurs eddy current and hysteresis loss in it. These two losses together are called Iron loss. It is 0 in ideal transformer.

When an alternating voltage V₁ is supplied to the primary winding of an ideal transformer, counter emf E₁ is induced in the primary winding. Since there is no resistance, this induced emf E₁ will be exactly equal to the applied voltage but in 180 degree opposite in phase.
The current drawn from the source produces required magnetic flux. As the primary winding resistance is 0, the current lags emf E₁ by 90 degree. This is current is called Magnetizing current I_μ. This magnetizing current produces alternating magnetic flux φ. This flux gets linked with the secondary winding and emf E₂ is induced by mutual induction. This E₂ is in phase with E₁. If the circuit is closed at secondary winding, then secondary current I₂ is produced. \[ E_1I_1 = E_2I_2 \]

Practical Transformer

In practical transformer, we have all sorts of losses that were 0 in ideal transformer like winding reistance, leakage flux, and iron losses, all are there.
Here we are gonna study two cases:
(a) No load
(b) On load

Practical Transformer on No Load

In no load transformer, the circuit on the secondary side is open.

V₁ is the primary voltage and I₁ is the primary current. Now I₁ has two components:
a) One component is responsible for generation of magnetic flux. This is called Magnetizing component of I₁ and is denoted by I_μ
b) Second component which is responsible for magnetic losses (Hysterisis and Eddy current losses) and primary winding losses. This is called Core loss component of I_c .
So its equivalent circuit diagram is:

where on primary side,

• V₁ is Primary Voltage
• R₁ is Primary Winding Resistance
• X₁ is Primary Leakage Reactance
• I₀ is No Load Primary Current
• I_c is Core Loss component of I₁
• I_μ is Magnetizing Component of I₁
• R_c is Core loss resistance
• X_m is Magnetizing Reactance
• N₁ is Number of turns in Primary Winding
• E₁ is Primary induced Emf

On secondary side:
• R₂ is Secondary winding resistance
• X₂ is Secondary leakage reactance
• N₂ is Secondary winding turns
• E₂ is Secondary induced emf
• V₂ is Secondary terminal voltage

Phasor Diagram

Explanation

First we will start with reference line which is common to both primary and secondary curcuit, here it is flux φ. Now using KVL in primary circuit
\( V_1 = -E_1 + I_0R_1 + jI_0X_1 \)
There is no direct relation between φ and V₁ so that we could directly draw phasor. But we have relation with E₁ and φ, as φ is responsible for both E₁ and E₂. E₁ and E₂ both lag φ by 90 degrees. Here we will consider E₁ < E₂.
φ is produced due to magnetizing current I_μ therefore I_μ is in phase with φ. As we have -E₁ in our equation (because it is in opposite direction of magnetizing current) so we will draw a phasor opposite to E₁.
I_c is 90 degrees leading from I_μ so it is in phase with -E₁ As I₀ = I_c + I_μ , hence the phasor I₀.
Now I₀R₁ is voltage drop in R₁ and it is in phase with I₀ , and as it is added to -E₁ so the phasor of I₀R₁ will be drawn at the head of -E₁. I₀X₁ is voltage drop across X₁ and is 90 degrees leading I₀R₁, so it is drawn perpendicular to I₀R₁.
Now following the equation, V₁ phasor is drawn adding all the quantities given in the equation.

Practical Transformer on Load

The secondary side is closed-circuited with a load.

Its equivalent circuit diagram:

where on primary side,

• V₁ is Primary Voltage
• I₁ is Primary Current
• I'₂ is Primary Current to neutralize the demagnitizing effects of I₂, I'₂ = K I₂
• I₀ is No Load Primary Current
• R₁ is Primary Winding Resistance
• X₁ is Primary Leakage Reactance
• I_c is Core Loss component of I₁
• I_μ is Magnetizing Component of I₁
• I'₁ component of I₁ (doubtful)
• R_c is Core loss resistance
• X_m is Magnetizing Reactance
• N₁ is Number of turns in Primary Winding
• E₁ is Primary induced Emf

On secondary side,
• R₂ is Secondary winding resistance
• X₂ is Secondary leakage reactance
• N₂ is Secondary winding turns
• E₂ is Secondary induced emf
• V₂ is Secondary voltage
• I₂ is Secondary current

Phasor Diagram

Explanation

Again we will start with refrence line, here it is φ.
Using KVL in secondary circuit,
\( V_2 = E_2 - I_2R_2 - jI_2X_2 \)
As there is no direct relation between V₁ and φ so we will use the equation to draw all three quantities and then add them to get V₁.
E₂ and E₁ lag φ by 90 degrees. Here we will consider E₂ < E₁. I₂ lags E₂ by phase difference of φ₂
Now voltage drop I₂R₂ across R₂ will be in phase with I₂ but we need -I₂R₂ so we will it in opposite direction of I₂. As it is to be added to E₂ so it will be drawn at the head of E₂.
I₂X₂ is voltage drop across X₂ and is leading by 90 degrees from I₂R₂. Again it is -ve in magnitude.
Adding all the quantities we have V₂.
Now in primary circuit,
V₁ = - E₁ + I₁R₁ + jI₁X₁
I₁ = I'₂ + I₀ where I'₂ = -KI₂
I₀ = I_μ + I_c
Again we will draw I_μ first as it is directly connected to φ, then I_c and then I₀ .
I'₂ is opposite to I₂ and is added to I₀. The resultant phasor is I₁.
I₁R₁ is in phase with I₁ and is added to -E₁. I₁X₁ is 90 degrees leading I₁R₁.
Phase difference between V₁ and I₁ is φ₁
Power Factor = cosφ₁
Input Power = V₁I₁cosφ₁

Phase difference between V₂ and I₂ is φ₂
Power Factor = cosφ₂
Input Power = V₂I₂cosφ₂

Equivalent Circuit of Transformer, Basic Electrical Engineering, Btech first year

Equivalent Circuit of Transformer

The concept of Equivalent Circuits exists to help us analyze transformer as by using this concept, we can transform all the parameters to either side. When referred to primary side, it is called Equivalent Circuit referred to primary side and when referred to secondary side, it is called Equivalent Circuit referred to secondary side.

Here \( I_1 = I_0 + I'_2 \)
The no load primary current \(I_0\) is very small in comparison to full load current around 2% to 5% of full load current. So, \[ I_1 \approx I'_2 \] So we will interchange the core loss and leakage flux loss part with the winding losses part as shown in the diagram. This is called Approximate Equivalent Circuit.

The core losses and flux losses are negligible, so we will remove them to further simply the circuit,

Now we can perform calculations:

Equivalent Circuit referred to Primary Side

This means shifting all the elements to the primary side.

\(R_{1e} \) is Equivalent resistance referred to primary
\(X_{1e} \) is Equivalent reactance referred to primary
Before we get into equations for equivalent resistance and reactance, get this formula for relation between resistance and turn ratio: \[ V_1 = I_1R_1 , V_2 = I_2R_2\] \[ \frac{V_1}{V_2} = \frac{I_1R_1}{I_2R_2} \] \[ \frac{R_1}{R_2} = \frac{V_1I_2}{V_2I_1} = \frac{N_1}{N_2}\frac{N_1}{N_2} \] \[ \frac{R_1}{R_2} = \left(\frac{N_1}{N_2} \right)^2 \] So if \(R_2\) is to be referred from secondary to primary side, then it will be written as \[ R_2\left(\frac{N_1}{N_2}\right)^2 \] And if \(R_1\) is to be referred from primary to secondary side, then it will be written as \[ R_1\left(\frac{N_2}{N_1}\right)^2 \] So writing equations for equivalent resistance and reactance, \[ R_{1e} = R_1 + R_2\left(\frac{N_1}{N_2} \right)^2 \] \[ X_{1e} = X_1 + X_2\left(\frac{N_1}{N_2} \right)^2 \]

Equivalent Circuit referred to Secondary Side

This means shifting all the elements to the secondary side.

\(R_{2e} \) is Equivalent resistance referred to secondary
\(X_{2e} \) is Equivalent reactance referred to secondary
\[ R_{2e} = R_2 + R_1\left(\frac{N_2}{N_1} \right)^2 \] \[ X_{2e} = X_2 + X_1\left(\frac{N_2}{N_1} \right)^2 \]

Auto Transformer, Basic Electrical Engineering, Btech first year

Auto Transformer

Auto Transformer is a transformer in which both primary and secondary side share same single winding i.e. one single winding is used as primary winding as well as secondary winding.

Here bc is called the common winding as it is shared by both primary and secondary sides. ab is called the series winding as it is in series with common winding.

Step Down Auto Transformer

Here \( V_H =\) High Voltage
\( V_L =\) Low Voltage
\( I_H =\) High Voltage Current
\( I_L =\) Low Voltage Current
\( T_{ac} =\) number of turns across ac
\( T_H =\) number of turns across high voltage side \(= T_{ac} \)
\( T_{bc} =\) number of turns across bc
\( T_L =\) number of turns across low voltage side \(= T_{bc} \)
\(T_{ab} =\) number of turns across ab
\( T_{ab} = T_H - T_L \) Also, \( I_H = I_{ab} \)
And when load is connected, \(I = I_{cb} \) Now in auto transformer, we study two types of ratios: Circuit Voltage Ratio (CVR) and Winding Voltage Ratio (WVR).
CVR is the ratio of voltages in primary and secondary circuits \[ CVR = \frac{V_H}{V_L} = \frac{T_H}{T_L} = a_A \Rightarrow \text{ Transformation Ratio } \longrightarrow (1) \] WVR is the ratio voltages in the windings of the primary and secondary sides \[ WVR = \frac{V_{ab}}{V_{bc}} = a \] I flows only when load is connected and flows in opposite direction of I_H. So the flux produced by I tries to reduce the flux produced by I_H but the value of flux by I_H is such that it nullifies the effect of flux by I. So the mmf by I_H becomes equal to the mmf by I. \[ I_{ab}T_{ab} = I_{bc}T_{bc} \] \[ I_H(T_H - T_L) = IT_L \] \[ \boxed{\frac{I}{I_H} = \frac{T_H - T_L}{T_L} = \frac{T_H}{T_L} - 1 = a_A - 1 } \longrightarrow (2) \] WVR: \[ a = \frac{V_{ab}}{V_{bc}} = \frac{T_{ab}}{T_{bc}} = \frac{T_H - T_L}{T_L} = \frac{T_H}{T_L} - 1 \] \[ \boxed{a = a_A - 1 } \longrightarrow (3) \] Applying KCL at point b \[ I_H + I = I_L \] \[ I = I_L - I_H \] \[ \frac{I}{I_H} = \frac{I_L - I_H}{I_H} \longrightarrow (4) \] From equation (2) \[ a_A - 1 = \frac{I_L - I_H}{I_H} \] \[ \boxed{a_A = \frac{I_L}{I_H} } \] \[ \Rightarrow \boxed{a_A = \frac{V_H}{V_L} = \frac{T_H}{T_L} = \frac{I_L}{I_H}} \] \[ \text{And } \boxed{a = a_A - 1} \]

Step Up Auto Transformer

All the calculations are same as in step down transformer, just the directions of currents change.

Saving in Conductor Material

As auto transformer uses single winding, it uses less matrial i.e. Copper in comparison to two winding transformers. To determine saving of Copper, we calculate weight of copper used.

Now the weight of copper used depends upon :

Current : because the flow of current depends upon the area of cross section of the turns of the winding. So larger the current means larger the area which in turn means more amount of Copper used

Number of Turns : larger the number of turns means more amount of Copper used.

For two winding transformer,
Weight of primary winding \( \propto N_1I_1 \)
Weight of secondary winding \( \propto N_2I_2 \)
Total Weight of Copper used \( \propto N_1I_1 + N_2I_2 \)
Weight of Copper in auto transformer \(\propto (N_1 - N_2)I_1 + N_2(I_2 - I_1) \) \[ \frac{\text{Weight of Copper in auto transformer}}{\text{Weight of Copper in ordinary transformer}} \] \[ = \frac{(N_1 - N_2)I_1 + N_2(I_2 - I_1)}{N_1I_1 + N_2I_2} \] \[ = \frac{N_1I_1 - N_2I_1 + N_2I_2 - N_2I_1}{N_1I_1 + N_2I_2} \] \[ = \frac{N_1I_1 - 2N_2I_1 + N_2I_2}{N_1I_1 + N_2I_2} \] As \(N_1I_1 = N_2I_2 \) \[ = \frac{2N_2I_2 - 2N_2I_1}{2N_2I_2} \] \[ = 1 - \frac{I_1}{I_2} \] \[ = \boxed{1 - K} \] \[\Rightarrow \text{Weight of copper in ordinary transformer} = (1 - K)\times\text{Weight of copper in auto transformer} \] So, Saving of Copper = Weight of copper in ordinary transformer - Weight of copper in auto transformer \[ = W_0 - (1 - K)W_0 \] \[ = W_0 - W_0 + KW_0 \] \[ \boxed{\text{Saving of Copper } = KW_0} \] When \(K \approx 1 \) saving is maximum

Advantages and Disdvantages

Due to single winding, it has lot of advantages when compared with 2 winding transformer and some disadvantages as well.

Advantages

a) In 2 winding transformer, transfer of energy occurs with the help of mutual induction only, but in auto transformer, due to single winding, energy transfer occurs through mutual induction as well as conduction of current.

b) Due to single winding, less material is used.

c) Due to single winding, leakage flux is very low.

d) Due to single winding, secondary winding resistance is very low.

e) It is of small size when compared to 2 winding transformer.

Disdvantages

a) If by mistake, the secondary side is open i.e. not connected to the winding, then all the high voltage will be transferred to the load, thus damaging the load.

b) Due to low impedance, an increase in short circuit current will damage the load.

Applications

a) In large power systems

b) In laborateries as variable transformer

c) Synchronous motor and induction motor are not self-starting, so it is used as a starter.

Transformers, Basic Electrical Engineering, Btech first year

Transformers

Topics that we are going to study in this unit:

Principle & Emf Equation Ideal & Practical Transformer Equivalent Circuit Losses & Efficiency Auto Transformer

AC Circuit-Single phase & 3 phase, Basic Electrical Engineering, Btech first year

AC Circuit

• Alternating Current & Alternating Voltage

  Definition : An Alternating Current in any circuit is current which varies both in magnitude and polarity with respect to time. Similarly, alternating voltage is voltage that varies both in magnitude and polarity with respect to time. The reversal of polarity of voltage or current occurs at regular intervals of time. The circuit in which AC flows is called Alternating Circuit.
  
  Equations : Consider a rectangular coil, having N turns and rotating in a uniform magnetic field, with an angular velocity of \(\omega\) \(radian/second\). Let \(\Phi _{m}\) be maximum flux linked with the coil and \(\Phi\) be flux linked with the coil at any time \(t\), then \[ \Phi = \Phi _m \cos{\omega t} \] According to Faraday's Law of Electromagnetic Induction, e.m.f. induced in the coil is given by rate of change of flux \[ e = -\frac{d}{dt}(N\Phi) = -N\frac{d}{dt}(\Phi _m \cos{\omega t}) \] \[ e = N\omega \Phi _m \sin{\omega t} \] For maximum e.m.f., \(\sin{\theta} = 1\) \[ E_m = N\omega \Phi _m \] \[ \boxed{e = E_m\sin{\omega t}} \] Similarly, \[ \boxed{i = I_m\sin{\omega t}} \]

• RMS Values & Average Values

  Average Values

  

  Instant Value = \(I_m \sin{\omega t}\)
  For whole cycle the average value will be \(0\) as the area under the first cycle is \(0\). So, taking first half of the cycle from \(0 \rightarrow \pi\) \[ I_{avg} = \int_{0}^{\pi} \frac{I_m\sin{\omega t}}{\pi - 0} d\omega t \] (as average = sum of instant values / no. of instant values) \[ I_{avg} = \frac{I_m}{\pi} \int_{0}^{\pi} \sin{\omega t} d\omega t \] \[ I_{avg} = \frac{I_m}{\pi} [-\cos{\omega t}]_0^{\pi} \] \[ \boxed{I_{avg} = \frac{2I_m}{\pi} } \] \[ \boxed{I_{avg} = 0.637I_m } \]
  
  Root Mean Square Values :
  \[ i = I_m\sin{\omega t} \] Squaring both the sides \[ i^2 = I_m^2 \sin^2{\omega t} \] \[ i^2 = I_m^2 \left(\frac{1 - \cos{\omega t}}{2} \right) \] Taking average of given value : \[ i_{avg}^2 = \frac{I_{m}^2}{2} \int_{0}^{\pi} \frac{1 - \cos{2\omega t}}{\pi}d\omega t \] \[ i_{avg}^2 = \frac{I_m^2}{2\pi} \left[ [\omega t]^{\pi}_0 - \left[ \frac{\sin{2\omega t}}{2} \right]^{\pi}_0 \right] \] \[ i_{avg}^2 = \frac{I_m^2}{2\pi} \times \pi \] \[ i_{av}^2 = \frac{I_m^2}{2} \] On taking square root \[ \boxed{i_{rms} = \frac{I_m}{\sqrt{2}}} \] \[ \boxed{ i_{rms} = 0.707I_m } \]

• Form Factor & Peak Factor

  Form Factor : Ratio of RMS value to the average value of altenating quantity \[ K_f = \frac{\text{RMS value}}{\text{Average value}} = \frac{E_{rms}}{E_{avg}} = \frac{\frac{E_m}{\sqrt{2}}}{\frac{2E_m}{\pi}} = 1.11 \]
  Peak Factor : Ratio of Peak or Maximum value to RMS value of an alternating quantity \[ K_p = \frac{\text{Max. value}}{\text{RMS value}} = \frac{E_m}{\frac{E_m}{\sqrt{2}}} = 1.414 \]

• Active & Reactive components of Circuit Current

  Active Component : \(I\cos{\phi} \longrightarrow\) the component which is in phase with the applied voltage \(V\) : also called as "Wattful component"
  Reactive Component : \(I\sin{\phi} \longrightarrow \) the component which is out of phase with the applied voltage : also called as "Wattless component"

  

• Power Factor & Quality Factor

  Power Factor : a) Cosine of the phase angle between \(V\) and \(I\) i.e. \(\cos{\phi} \) b) Ratio of Resistance to Impedance \[ \cos{\phi} = \frac{R}{Z} \] c) Ratio of active power to apparent power \[ \cos{\phi} = \frac{\text{Active Power}}{\text{Apparent Power}} \] Note : P.F. cannot be greater than 1
  
  Quality Factor : Reciprocal of Power factor is Quality Factor \[ \text{Q-factor } = \frac{1}{\cos{\phi}} = \frac{Z}{R} \] Also, \[ \text{Q-factor } = 2\pi \frac{\text{Max. Energy stored}}{\text{Energy dissipated per cycle}} \]

• Active, Reactive & Apparent Power

  Apparent Power : the product of RMS values of applied voltage and circuit current \[ S = V_{rms}I_{rms} \] \[ \text{Unit : Volt-Ampere (VA) } \] Active Power : the product of apparent power and the power factor
  it is due to the resistive part of the circuit \[ P = V_{rms}I_{rms}\cos{\phi} \] \[ \text{Unit : Watts (W)} \] Reactive Power : the product of apparent power and the sin of phase difference between \(V\) and \(I\)
  also called as "Wattless Power" \[ Q = V_{rms}I_{rms}\sin{\phi} \] \[ \text{Unit : Volt-Ampere-Reactive (VAR) } \]

• AC Circuit containing purely Resistive load

  Let us assume that a purely resistive load \(R \omega\) is connected across a supply of \( V = V_m\sin{\omega t} \longrightarrow (1) \)

  

  \[ i = \frac{V}{R} \hspace{20pt} \text{[Ohm's law]} \] Putting value of \(V\) from (1) \[ i = \frac{V_m\sin{\omega t}}{R} \] \[ \boxed{i = I_m\sin{\omega t} } \longrightarrow (2) \] Comparing (1) and (2)
  Voltage and Current are in same phase. Its phasor diagram is,

  

  Power Dissipated : \[ P = Vi \] Putting values of \(V\) and \(i\) in \[ P = V_m\sin{\omega t} \times I_m\sin{\omega t} \] \[ P = V_mI_m\sin^2{\omega t} \] \[ P = V_mI_m \left( \frac{1 - \cos{2\omega t}}{2} \right) \] \[ P = \frac{V_mI_m}{2} - \frac{V_mI_m\cos{2\omega t}}{2} \] Neglecting the fluctuating part \[ P = \frac{V_mI_m}{2} \] \[ P = \frac{V_m}{\sqrt{2}} \frac{I_m}{\sqrt{2}} \] \[ \boxed{P = V_{rms}I_{rms}} \]

• AC Circuit containing purely Inductive load

  Let us assume that a purely inductive load to be connected in series across voltage supply of \(V = V_m\sin{\omega t} \longrightarrow (1)\)

  

  e.m.f. induced is given as: \[ v = L\frac{di}{dt} \] \[ V_m\sin{\omega t} = L\frac{di}{dt} \] \[ \int \frac{V_m\sin{\omega t}}{L}dt = \int di \] \[ i = \frac{V_m}{L} \int \sin{\omega t}dt \] \[ i = \frac{V_m}{L} \left( \frac{-\cos{\omega t}}{\omega} \right) \] \[ i = \frac{V_m}{\omega L} \sin{(\omega t - \pi /2)} \] Comparing it to Ohm's Law \[ \boxed{X_L = \omega L} \] \[ i = \frac{V_m}{X_L} \sin{(\omega t - \pi /2)} \] \[ \boxed{i = I_m\sin{(\omega t - \pi /2)}} \] For purely inductive load \(I\) lags behind \(V\) by \(90^\circ\). Its phasor diagram is,

  

  Power : \[ P = VI \] \[ P = V_m\sin{\omega t}I_m\sin{(\omega t - \pi /2)} \] \[ P = -V_mI_m\sin{\omega t}\cos{\omega t} \] \[ P = -2 \times \frac{V_mI_m\sin{\omega t}\cos{\omega t} }{2} \] \[ P = \frac{-V_mI_m}{2}\sin{2\omega t} \] Neglecting the fluctuating part \[ \boxed{P = 0} \]

• AC Circuit containing purely Capacitive load

  Let us assume that a purely capacitive load of capacitance \(C\) \(F\) to be connected in series across voltage supply of \(V = V_m\sin{\omega t} \longrightarrow (1)\)

  

  The charge stored by capacitor is given as \[ q = CV \] \[ i = \frac{dq}{dt} \] \[ i = C\frac{dV}{dt} \] \[ i = C\frac{d}{dt}V_m\sin{\omega t} \] \[ i = CV_m\omega \cos{\omega t} \] \[ i = \omega CV_m\sin{(\omega t + \pi /2)} \] Comparing with Ohm's Law \[ \boxed{X_C = \frac{1}{\omega C} = \frac{1}{2\pi fC} } \] \[ i = \frac{V_m}{X_C}\sin{(\omega t + \pi /2)} \] \[ \boxed{i = I_m\sin{(\omega t + \pi /2)}} \longrightarrow (2) \] For purely Capacitive load, current \(I\) leads \(V\) by \(90^\circ \). Its phasor diagram is,

  

  Power : \[ P = Vi \] \[ P = V_m\sin{\omega t}I_m\sin{(\omega t + \pi /2)} \] \[ P = V_mI_m\sin{\omega t}\cos{\omega t} \] \[ P = 2 \times \frac{V_mI_m\sin{\omega t}\cos{\omega t}}{2} \] \[ P = \frac{V_mI_m}{2}\sin{2\omega t} \] Neglecting fluctuating part \[ \boxed{P = 0} \]

• R-L Circuit

  Consider a circuit consisting of resitor \(R\) and an inductive coil of inductance \(L\) connected in series. Since it includes inductor \(I\) will lag behind \(V\) by some phase difference \(\phi\) \[V = V_m\sin{\omega t}, i = I_m\sin{(\omega t - \phi)} \]

  

  \[ V = \sqrt{V_L^2 + V_R^2} \] \[ V = \sqrt{(IR)^2 + (X_L)^2} \] \[ V = I\sqrt{R^2 + X_L^2} \] \[ V = IZ \] \[ \text{Impedance, } Z = \sqrt{R^2 + X_L^2} \] \[ \tan{\phi} = \frac{V_L}{V_R} = \frac{X_L}{R} \] \[ \boxed{ \phi = \tan^{-1}{\frac{X_L}{R}} } \] Power Factor : \[ \boxed{\cos{\phi} = \frac{R}{Z} } \] \[ \boxed{P = VI\cos{\phi}} \]

  
  

  Sample Problem :

  A \(4\Omega\) resitor is connected to \(10mH\) inductor across \(100V, 50Hz\) voltage source in series. Find
  (a) Input current
  (b) Voltage drop across inductor and resistor
  (c) Power Factor
  (d) Power consumed

  Solution :

  

  \[ R = 4\Omega, L - 10mH, X_L = \omega L = 2\pi fL \] \[ X_L = 2\pi \times 50 \times 10 \times 10^{-3} = 3.142\Omega \] \[ z = \sqrt{R_2 + X_L^2} \] \[ = \sqrt{4^2 + (3.142)^2} \] \[ = 5.086\Omega \] (a) Input Current : \[ I = \frac{V}{Z} = \frac{100}{5.086} = 19.66A \] (b) Voltage Drop across Resistor \[ I = 19.66A \] \[ V_R = IR = 19.66 \times 4 \] \[ V = 78.64V \] Voltage Drop across Inductor : \[ V_L = IX_L = 19.66 \times 3.142 \] \[ V_L = 61.77V \] (c) Power Factor \[ = \frac{R}{Z} = \frac{4}{5.086} = 0.786 \] (d) Power consumed = \[ VI\cos{\phi} = 100\times 19.66 \times 0.786 \] \[ = 1546W \]

• R-C Circuit

  Consider a circuit consisting of resitor \(R\) and a capacitor of capacitance \(C\) connected in series. Since it includes capacitor \(I\) leads \(V\) by some phase difference \(\phi\) [V = V_m\sin{\omega t}, i = I_m\sin{(\omega t + \phi)} \]

  

  \[ V = \sqrt{V_C^2 + V_R^2} \] \[ V = \sqrt{(IR)^2 + (X_C)^2} \] \[ V = I\sqrt{R^2 + X_C^2} \] \[ V = IZ \] \[ \text{Impedance, } Z = \sqrt{R^2 + X_C^2} \] \[ \tan{\phi} = \frac{V_C}{V_R} = \frac{X_C}{R} = \frac{1}{\omega CR} \] \[ \boxed{ \phi = \tan^{-1}{\frac{X_C}{R}} } \] Power Factor : \[ \boxed{\cos{\phi} = \frac{R}{Z} } \] \[ \boxed{P = VI\cos{\phi}} \]

• R-L-C Circuit

  

  \[ V = IR, \] \[V_L = IX_L, \hspace{10pt} \text{ V leads I by }\pi /2 \] \[ V_C = IX_C, \hspace{10pt} \text{I leads V by }\pi /2 \] If \(V_L\) > \(V_C\), \[ V = \sqrt{(V_R)^2 + (V_L - V_C)^2} \] \[ V = \sqrt{IR^2 + (IX_L - IX_C)^2} \] \[ V = I \sqrt{R^2 + (X_L - X_C)^2} \] \[ \boxed{Z = \sqrt{ R^2 + (X_L - X_C)^2 }} \] If \(X_C > X_L\) or \(V_C > V_L\) \[ \boxed{Z = \sqrt{ R^2 + (X_C - X_L)^2 }} \] \[ \tan{\phi} = \frac{V_L - V_C}{V_R} \] \[ \boxed{\phi = tan^{-1}\frac{V_L - V_C}{V_R} = \tan^{-1}\frac{X_L - X_C}{R} } \] Power factor : \[ \cos{\phi} = \frac{R}{Z} \] \[ \cos{\phi} = \frac{R}{\sqrt{R^2 + (X_L - X_C)^2}} \] Power consumed, \[ \boxed{P = VI\cos{\phi}} \]

• Three Phase AC Circuit

  We study two types of connections in 3 phase systems: Star and Delta connection.

  Star Connection

  All the three terminals are connected to a common point. Also called as Y connection.

  

  Line Currents : \(I_A = I_B = I_C = I_L \)
  Line Voltages : \(V_{AB} = V_{AC} = V_{BC} = V_L \)
  Phase Currents : \(I_{NA} = I_{NB} = I_{NC} = I_{P} \)
  Phase Voltages : \(V_{A} = V_{B} = V_{C} = V_{P} \)
  
  

  Relationship between Line and Phasor Currents

  As we can see from the diagram \[ I_{NA} = I_A \] \[ I_{NC} = I_C \] \[ I_{NB} = I_B \] \[ \Rightarrow \boxed{I_P = I_L} \]

  Relationship between Line and Phasor Voltages

  

  \[ V_{AB} = V_A - V_B \] \[ = \sqrt{(V_A)^2 + (V_B)^2 + 2V_AV_B\cos{60^o}} \] \[ = \sqrt{V_A^2 + V_B^2 + V_AV_B} \] As \(V_A = V_B = V_C \) \[ V_{AB} = \sqrt{3V_A^2} = \sqrt{3}V_A \] \[ \Rightarrow \boxed{V_L = \sqrt{3}V_P} \] Power : Active Power in 1 phase = \(V_PI_P\cos{\phi}\)
  Active Power in 3 phase, \[ P_T = 3V_PI_P\cos{\phi} \] \[ V_P = \frac{V_L}{\sqrt{3}}, I_P = I_L \] \[ P_T = 3\frac{V_L}{\sqrt{3}}I_L\cos{\phi} \] \[ \boxed{P_T = \sqrt{3}V_LI_L\cos{\phi} } \] Reactive Power : \[ Q_T = \sqrt{3}V_LI_L\sin{\phi} \] Apparent Power : \[ S_T = \sqrt{3}V_LI_L \]

  
  

  Delta Connection

  

  Line Currents : \(I_A = I_B = I_C = I_L \)
  Line Voltages : \(V_{AB} = V_{AC} = V_{BC} = V_L \)
  Phase Currents : \(I_{AB} = I_{AC} = I_{BC} = I_{P} \)
  Phase Voltages : \(V_{A} = V_{B} = V_{C} = V_{P} \)
  
  

  Relationship between Line and Phasor Voltages

  As we can see from the diagram \[ V_{A} = V_{AC} \] \[ V_{B} = V_{AB} \] \[ V_{C} = V_{BC} \] \[ \Rightarrow \boxed{V_L = V_P} \]

  Relationship between Line and Phasor Currents

  

  \[ I_A = I_{AC} - I_{AB} \] \[ = I_{AC} + (-I_{AB}) \] \[ = \sqrt{I_{AC}^2 + I_{AB}^2 + 2I_{AC}I_{AB}\cos{60^o}} \] As \(I_{AC} = I_{AB} = I_{BC} \) \[ \Rightarrow I_A = \sqrt{3I_{AC}^2} = \sqrt{3}I_{AC} \] \[ \Rightarrow \boxed{I_L = \sqrt{3}I_P} \] Power : Active Power in 1 phase = \(V_PI_P\cos{\phi}\)
  Active Power in 3 phase, \[ P_T = 3V_PI_P\cos{\phi} \] \[ I_P = \frac{I_L}{\sqrt{3}}, V_P = V_L \] \[ P_T = 3V_L\frac{I_L}{\sqrt{3}}\cos{\phi} \] \[ \boxed{P_T = \sqrt{3}V_LI_L\cos{\phi} } \] Reactive Power : \[ Q_T = \sqrt{3}V_LI_L\sin{\phi} \] Apparent Power : \[ S_T = \sqrt{3}V_LI_L \]